[초등수학 3-2] '2. 나눗셈' 단원 대표 유형 문제 풀어보기

[초등수학 3-2] '2. 나눗셈' 단원 대표 유형 문제 풀어보기

 

 

초등학생 때 아이의 수학 실력을 결정하는 것은 무엇일까요?

개념과 원리를 잘 알고 있는 것일까요? 아닙니다.

연산(계산)을 잘 하는 것일까요? 아닙니다.

​

둘 다 중요한 항목이지만 아이의 수학 실력을 결정하는 것은 아닙니다.

개념과 원리만 잘 알고 있다고 해서 좋은 성적을 얻게 되는 것도 아니고요.

연산(계산)을 잘 한다고 해서 좋은 성적을 얻게 되는 것도 아닙니다.

​

최종적으로 아이의 수학 실력을 결정하는 것은 '문제 해결 능력' 입니다.

그래서 다양한 유형과 적절한 난이도의 문제들을 충분히 풀어보는 것이 매우 중요한데요.

​

이는 초등뿐만 아니라 중등과 고등 때에도 마찬가지이고요.

학교 내신 시험이나 수능 시험 때에도 마찬가지입니다.

그리고 다양한 유형의 문제를 풀어볼 때에는 먼저 각 단원별 대표 유형 문제들부터 잘 풀어봐야 합니다.

 

 

 

 

아래 문제들은 초등학교 3학년 2학기 수학 2단원인 '2. 나눗셈' 단원에서 대표 유형에 해당하는 문제들입니다.

 

첫 번째 문제는 전국 기준으로 난이도 중보다 쉬운 문제입니다.

따라서 이 문제는 쉽게 또는 무난하게 풀 수 있어야 합니다.

 

그에 비해 2~4번 문제는 전국 기준으로 난이도 중 또는 그 위 수준의 문제입니다.

따라서 이 두 문제도 쉽게 푼다면 전국 기준 상위권일 확률이 높고요.

좀 끙끙거리더라도 풀어내면 상위권에 도전해볼만한 수준일 것입니다.

 

물론 아래 4문제 말고도 대표 유형 문제는 더 있는데요.

일단 이 문제들을 통해 현재 아이의 문제 해결 능력을 체크해 보시기 바랍니다.

 

 

대표 유형 문제 1 - 난이도 중하

 

 

77 ÷ 6 = 12 나머지 5

몫은 두 자리 수 12입니다. (영민 맞음)

나머지는 6보다 작은 5입니다. (지원 틀림)

나누어떨어지지 않습니다. (하정 틀림)

 

<정답> 영민

 

대표 유형 문제 2 - 난이도 중

 

 

가로등 사이의 간격 수 = 84 ÷ 7 = 12(군데)

한쪽에 세우는 가로등 수 = 12 + 1(처음 시작하는 곳) = 13개

양쪽에 세우는 가로등 수 = 26개

 

<정답> 26개

 

대표 유형 문제 3 - 난이도 중상

 

 

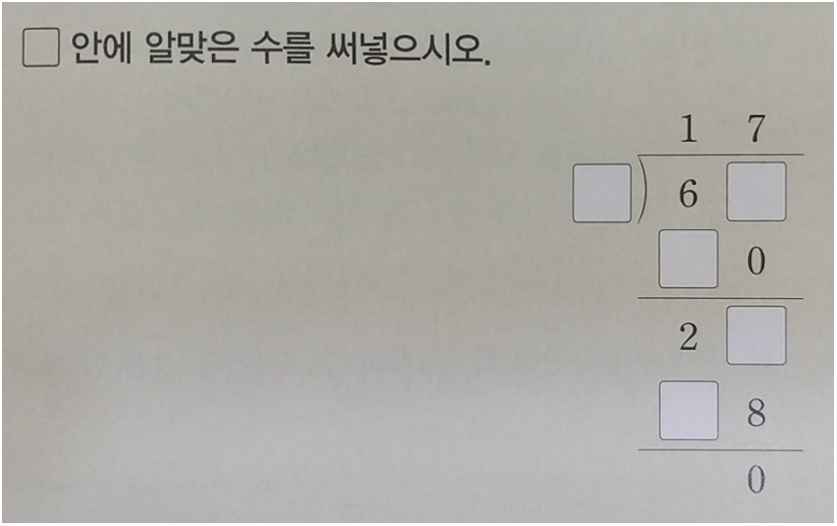
제일 아래 2□ 빼기 □8 이 0이므로 28-28 이 됩니다.

6□ - □0 = 28 이므로 68 - 40 이 됩니다.

 

<정답> 위에서부터 순서대로 4, 8, 4, 8, 2

 

대표 유형 문제 4 - 난이도 중상

 

 

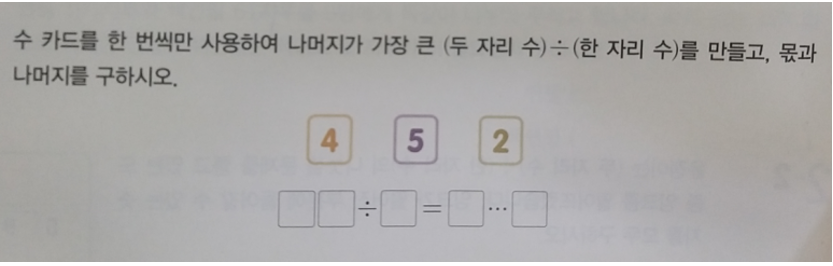
세 장의 수 카드로 만들 수 있는 나눗셈식을 모두 구하면

45 ÷ 2 = 22 나머지 1

54 ÷ 2 = 27

42 ÷ 5 = 8 나머지 2

24 ÷ 5 = 4 나머지 4

52 ÷ 4 = 13

25 ÷ 4 = 6 나머지 1

 

<정답> 24 ÷ 5 = 4 나머지 4