초등학교 수학 문제집은 종류가 참 많습니다.
수 많은 문제집 중에서 어느 것을 고를지도 고민이고요.
지금 하는 문제집 다음에 어느 문제집을 하면 좋을지도 고민인데요.
그래서 미래엔 출판사의 초등 수학 문제집 4가지를 활용하는 방법을 정리했습니다.
4가지 문제집은 '수학중심, 유형맞짱, 문제 해결의 길잡이 원리, 문제 해결의 길잡이 심화' 입니다.

4가지 문제집 모두 초등수학 내신 대비 문제집이고요.
가장 먼저 해야 할 것은 전국 기준 해당 문제집의 난이도를 확인하는 것입니다.
난이도 구분은 1, 2, 3, 4, 5단계로 하는 게 좋은데요.
- 난이도 1 : 기본, 기초, 개념 (난이도 하하)
- 난이도 2 : 기본과 실전의 중간 (난이도 중하)
- 난이도 3 : 응용, 실전 (난이도 중중)
- 난이도 4 : 실전과 심화의 중간, 준심화 (난이도 중상)
- 난이도 5 : 심화 (난이도 상상)
[수학중심] ⇒ 난이도 2 ⇒ 1과 3 중 1에 더 가까움

이 문제집은 기본 위주이면서 실전을 일부 고려한 문제집으로 보이고요.
이 문제집에서 어려운 문제의 난이도는 이 정도입니다.
[문제 사례 1] 어떤 수에 346을 더해야 할 것을 잘못하여 364를 더했더니 521이 되었습니다. 바르게 계산한 값을 구해 보세요.
[문제 사례 2] 종이배를 은지는 283개, 대호는 432개 접었고, 민수는 대호보다 164개 적게 접었습니다. 세 사람이 접은 종이배는 모두 몇 개인지 풀이 과정을 쓰고 답을 구해 보세요.
사실 위 문제는 풀 수 있어야 합니다. 그런데 기초를 충분히 하면서 위와 같은 문제가 일부 나옵니다. 그래서 이 문제집은 수학 공부를 적게 한 아이, 기초부터 탄탄하게 다져야 하는 아이에게 적합해 보이고요. 초등 수학 문제집 기본서로 완성도는 좋아 보입니다.
[유형맞짱] ⇒ 난이도 2 ⇒ 1과 3 중 3에 더 가까움

이 문제집은 기본도 다루지만 실전을 더 고려한 문제집으로 보입니다. '유형 공략하기' 라는 코너가 별도로 있을 정도이고요. 그리고 이 문제집에서 어려운 문제의 난이도는 이 정도입니다.
[문제 사례 1] 기차가 서울역에서 출발하여 대전역에 한 번 정차한 후 다시 경주역으로 가고 있습니다. 대전역에서 286명이 내리고, 456명이 탔더니 지금 기차에 타고 있는 사람이 951명입니다. 서울역에서 출발할 때 기차에 타고 있던 사람은 몇 명일까요?
[문제 사례 2]
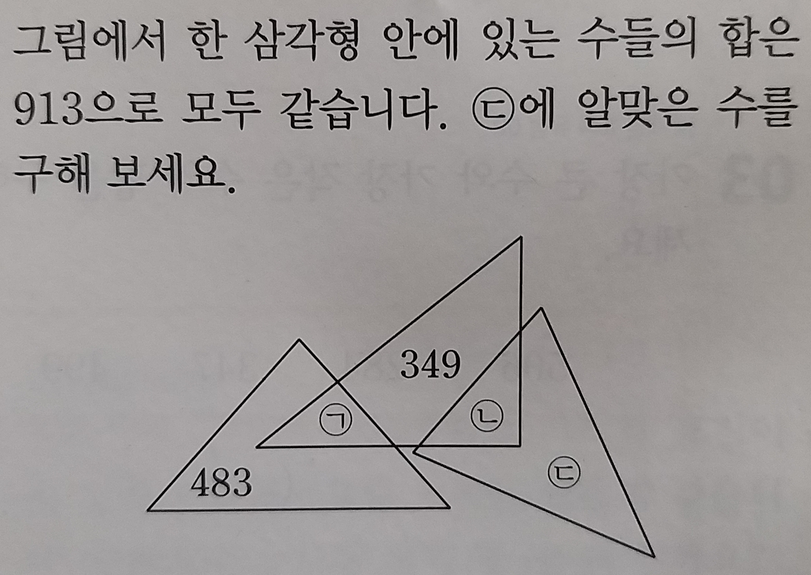
이때 유형맞짱의 난이도를 수학중심보다 더 높게 보는 이유는, 전반적으로 문제의 난이도가 높기 때문이 아니라 문제 수가 많기 때문입니다.
따라서 두 문제집 모두 첫 번째 문제집으로 선택할 수 있고요.
좀 가볍게, 부담 없이 진행하고자 한다면 수학중심이 좋으며, 문제를 좀 많이 풀리면서 기초와 유형 공부를 확실하게 하고자 한다면 유형맞짱이 더 좋아 보입니다.
[문제 해결의 길잡이 원리] ⇒ 난이도 3~4 ⇒ 3에 더 가까움

문제 해결의 길잡이는 줄여서 '문해길'이라 부르는데요. 원리편이 있고, 심화편이 있습니다.
원리편는 학기 교재, 심화편은 1년 교재이고요. 심화편이 더 어렵습니다.
문해길 원리편의 난이도는 전국 기준 3(실전)~4(준심화) 사이로 보이며, 4보다는 3에 더 가깝습니다.
난이도 1의 기초 문제는 거의 없으며, 난이도 2 문제 좀 있고, 난이도 3 정도의 문제가 많으며, 난이도 3 이상의 문제가 좀 있습니다.
이 문제집에서 어려운 문제의 난이도는 이 정도입니다.
[문제 사례 1] 다음 조건을 만족하는 세 자리 수는 모두 몇 개입니까?
- 백의 자리 수와 십의 자리 수가 같습니다.
- 짝수입니다.
[문제 사례 2] 광현이의 할머니네 농장에는 오리와 염소가 합하여 50마리 있습니다. 광현이가 농장에 있는 오리와 염소의 다리를 세어 보았더니 모두 150개였습니다. 오리는 몇 마리입니까?
전국 기준 수학 상위권 아이라면 교과서로 개념 공부를 한 다음에 이 문제집으로 바로 들어가도 괜찮습니다. 하지만 그런 아이들은 소수이고요.
아래 난이도의 문제집을 한 후 이 문제집을 두 번째로 선택하는 것이 좋습니다. 특히 저학년과 중학년 아이일수록 차근차근 진행하는 것이 좋습니다.

[문제 해결의 길잡이 심화] ⇒ 난이도 4~5

문해길 심화편은 전국 기준 난이도 4~5로 보이며, 난이도 3과 4의 문제가 많아 보입니다. 예를 들면 이런 문제들입니다.
[문제 사례 1] 부산행 기차가 서울역에서 출발하여 대전역에서 125명이 내리고 143명이 기차에 탔습니다. 다음 대구역에서 89명이 내리고 탄 사람은 없습니다. 마지막 부산역에서 내린 사람이 334명일 때 처음 서울역에서 기차가 출발할 때 타고 있던 사람은 몇 명입니까?
[문제 사례 2]

따라서 학기 공부를 할 때 처음부터 문해길 심화를 할 수 있는 아이들은 소수이고요. 해당 학기 공부의 두 번째 문제집으로 고려해 볼만 합니다. 단, 난이도가 높기 때문에 모든 아이들에게 적용할 수는 없습니다.
[아이별 문제집 선택 사례]
위 문제집 4가지를 차근차근 다 풀면 좋을까요? 아닙니다.
문제 수도 너무 많고, 내 아이에게는 너무 쉽거나 너무 어려운 문제일 수도 있습니다.
저는 학기 당 내신 문제집 2권 진행을 기본으로 추천하고요. 경우에 따라 특정 단원 또는 추가 문제집에서 난이도 높은 문제만 더 풀어보는 것을 추천합니다.
그래서 위 4가지 문제집도 다 풀리는 것보다는 아이에 맞게 2가지 정도를 선택하는 것이 좋은데요.
기초부터 탄탄히 해야 하는 아이라면 당연히 수학중심이나 유형맞짱 중 하나를 선택하고요. 수학중심을 했는데 쉽지 않았다면 유형맞짱으로 보충하는 것이 좋습니다.
수학중심이나 유형맞짱을 선택했는데 잘 풀었다면 문해길 원리를 해 보고요. 만약 문해길 원리도 잘 했다면 심화에 도전해 보는 것이 좋습니다.
만약 수학중심이나 유형맞짱을 아주 쉽게 푸는 아이라면 차라리 처음부터 문해길 원리를 해 보는 것도 괜찮은 방법이고요. 이 경우 두 번째 문제집으로 문해길 심화를 진행하면서 문제해결력을 심화 수준까지 끌어올리는 것이 좋습니다.

내 아이의 수학 실력은 어디에서 판가름날까요?
대학에서는 아이의 수학 실력을 무엇으로 판단할까요?
연산(계산) 능력? 아닙니다!
사고력 수학? 아닙니다!
경시대회 성적? 아닙니다!
교과서 기반의 내신 문제해결력으로 판단하고요. 그것이 내신 성적입니다!
그럼 어떻게 해야 할까요? 결국은 전국 기준 난이도 상의 내신 문제집을 풀어내야 합니다!
우리나라에서 수학 공부 잘 하게 해서 기왕이면 좋은 대학에 보내고 싶으신가요?
그렇다면 우선 수학 공부 방향부터 잘 잡으시기 바라고요.
제가 진행하는 강.의, 컨설티 등을 활용해 보세요. 많은 궁금증이 해결되실 거예요 ^^
[강.의안내] 초등공부 변화와 대비법 (2022교육과정과 2028대입안 분석)
https://blog.naver.com/jnanna89/223528975599
[강.의안내] 초등공부 변화와 대비법 (2022교육과정과 2028대입안 분석)
2022 개정교육과정이 시작되었습니다. 교육부에서는 2028년 대입개편안을 발표했습니다. 대학들이 큰 변화...
blog.naver.com
온라인 오프라인 '전국 컨설팅' 을 진행합니다!
https://blog.naver.com/jnanna89/223411183581
온라인 오프라인 '전국 컨설팅' 을 진행합니다!
안녕하세요! 정용호 강사입니다! 1:1 맞춤으로 아이 공부 플랜을 정리해 드리는 컨설팅을 진행합니다. ∎ (...
blog.naver.com


'행공신 정보 > 문제집 비교분석' 카테고리의 다른 글
| [초등수학문제집추천] 디딤돌 초등수학 내신 문제집 (1) | 2024.08.01 |
|---|---|
| [초등한자 교재소개] 미래엔 하루 한장 한자 (한자검정능력시험 대비) (0) | 2024.07.31 |
| [초등 영어문법 교재] '하루한장 초등 영문법' 소개 (0) | 2024.07.28 |
| 초등수학 문장제 연습 문제집 3종 난이도 비교 (0) | 2024.07.14 |
| 초등수학문제집 중 '문해길-원리'는 어떤 아이들에게 좋을까? (2) | 2024.07.13 |




댓글