[초등수학 4-2] '3. 소수의 덧셈과 뺄셈' 교과서 핵심 원리
초등 4학년 2학기 수학 3단원은
'3. 소수의 덧셈과 뺄셈' 단원입니다.
이 단원에서 배우는 원리는 두 자리 수 덧셈과 뺄셈,
세 자리 수 덧셈과 뺄셈 원리와 거의 비슷합니다.
수의 크기가 다를 뿐이고요.
받아올림이나 받아내림 원리 적용은 똑같습니다.
<초등 4학년 2학기 수학 6개 대단원>
1. 분수의 덧셈과 뺄셈
2. 삼각형
3. 소수의 덧셈과 뺄셈
4. 사각형
5. 꺾은선그래프
6. 다각형
그래서 지금까지 수학 공부를 잘 해 왔다면,
이 단원 교과서 공부는 쉽게 할 수 있습니다.
그리고 이 단원에 해당하는 연산 연습도 많이 할 필요 없습니다.
절대! 많이 할 필요 없습니다.
대신 내신 문제집 2권 풀면서 내신 문제 해결력은 잘 훈련해야 합니다.
이 단원은 내신 문제의 난이도를 다양하게 할 수 있기 때문입니다.
우선 교과서 원리 공부부터 완벽하게 한 다음!
내신 문제 해결력을 탄탄하게 기르는 것이 핵심이고요!
수학 잘 하면, 난이도 중 아래 문제는 조금만 푸는 게 좋습니다!
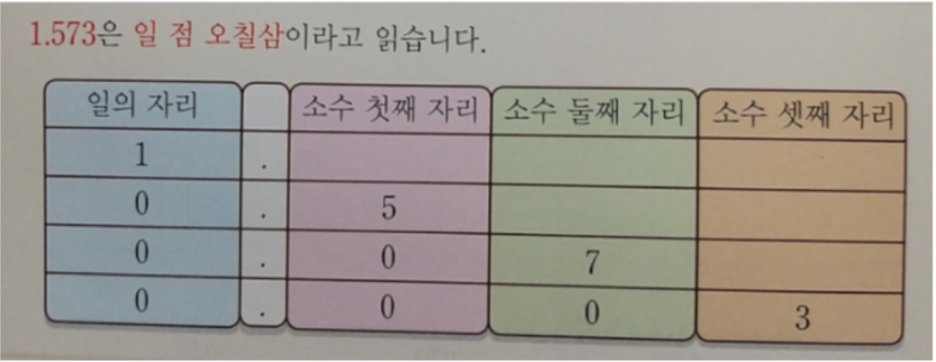
아래 교과서 내용은 '영 점 영일'의 개념인데요.
역시나 교과서나 문제집에 있는 개념 정리는 결론 위주이고 사전식입니다.
하나(전체)를 100개로 조각낸 것 중 한 조각을 '0.01'이라 쓰고 '영 점 영일' 이라고 읽습니다.
이때 옆에 있는 그림을 함께 보면서 0.01이 얼만큼의 양을 의미하는지 확인해야 합니다.

아래 내용은 구체적인 사례 하나로 소수의 개념을 학습하는 내용입니다.
0.85(영 점 팔오)는 하나(전체)를 10개로 조각낸 것 중 한 조각짜리가 8개 있고,
100개로 조각낸 것 중 한 조각짜리가 5개 있는 것입니다.

아래 내용은 자릿값 개념을 소수에 적용하는 내용인데요.
소수 첫째 자리는 하나(전체)를 10개로 조각낸 것 중 한 조각짜리가 몇 개 있는지를 쓰는 자리이고,
소수 둘째 자리는 하나(전체)를 100개로 조각낸 것 중 한 조각짜리가 몇 개 있는지를 쓰는 자리입니다.
(교과서나 문제집에는 이렇게 설명되어 있지 않습니다..)

계속 구체적인 사례를 통해 개념을 공부하는 내용이 나옵니다.
0.01을 열 개로 조각낸 것 중 한 조각을 0.001이라 쓰고 '영 점 영영일'이라고 읽습니다.
이렇게 이해하는 것이 더 쉽습니다.

위 교과서 내용을 제대로 공부했다면 아래 내용은 쉽게 이해할 수 있고요.

자릿값 개념을 소수 셋째 자리까지 확장해서 공부하는 내용입니다.
소수 셋째 자리는 하나(전체)를 1000개로 조각낸 것 중 한 조각짜리가 몇 개인지를 쓰는 자리입니다.
이제 소수 덧셈의 원리를 이해하는 내용입니다.
하나(전체)를 10개로 조각낸 것 중 한 조각짜리가 9개 있고,
하나(전체)랑 하나(전체)를 10개로 조각낸 것 중 한 조각짜리가 4개 있습니다.
모두 더해야 하고요.
10개로 조각낸 것 중 한 조각짜리가 9개와 4개 있으니까 하나가 생기고 남은 0.1 조각은 3개입니다.
그래서 2.3 입니다.
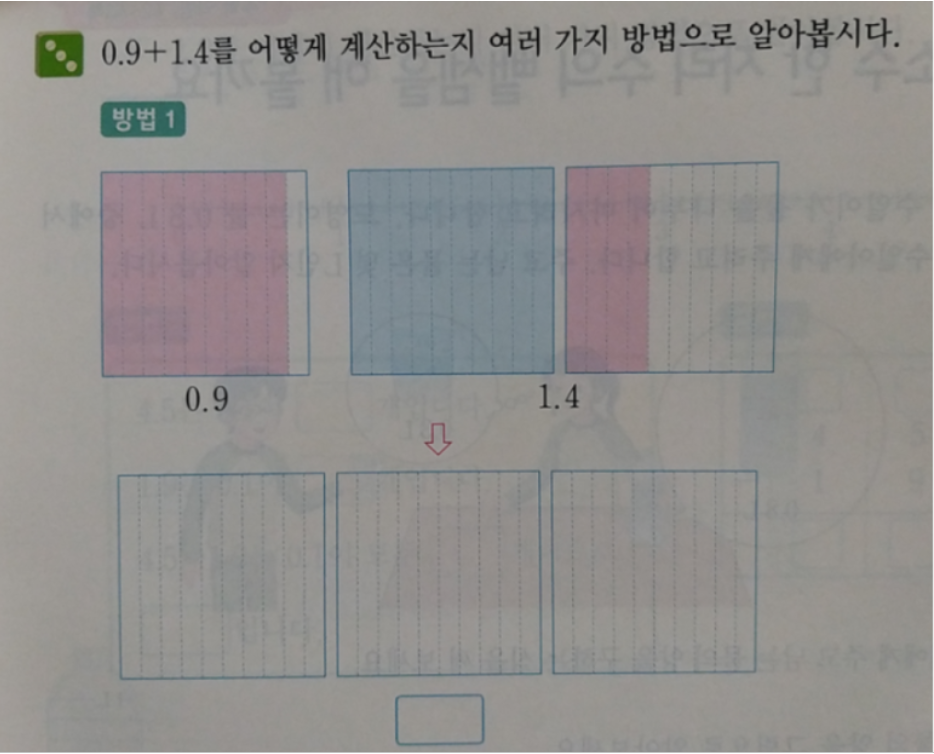
그 다음에는 여러 가지 방법으로 계산하기입니다.
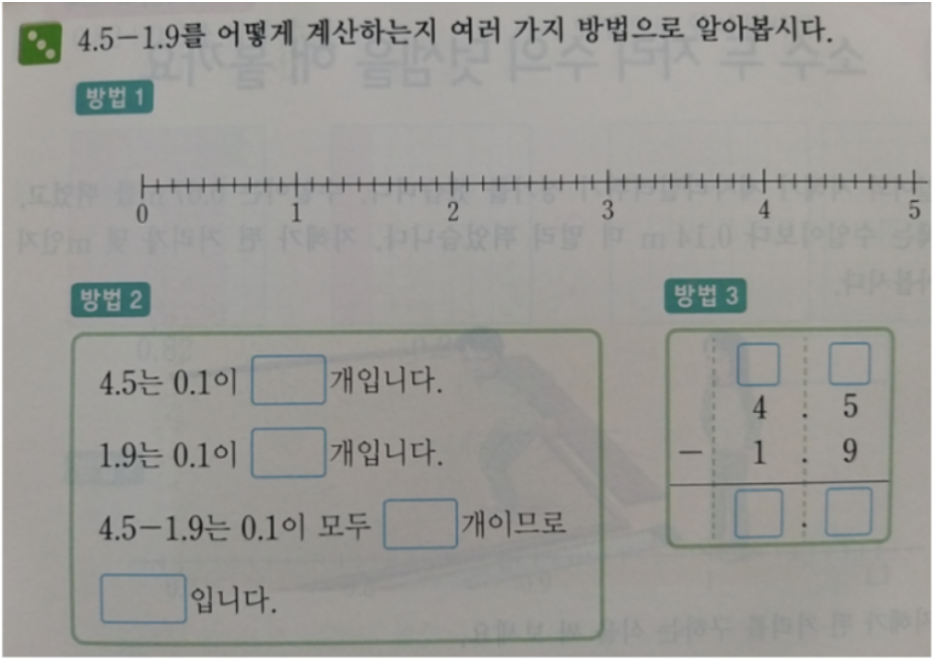
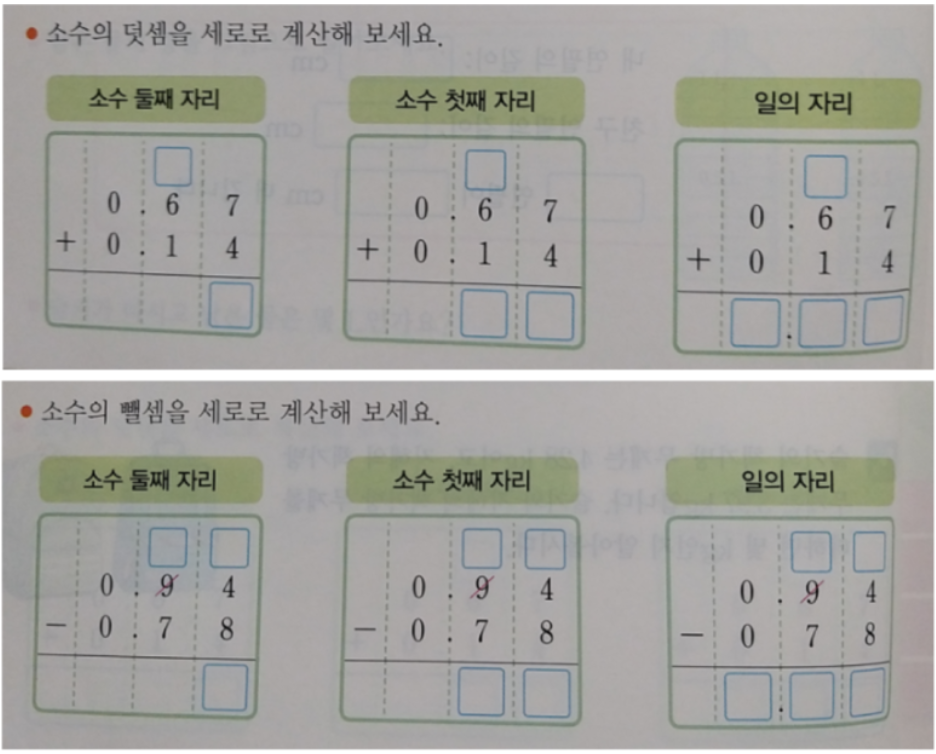
이제 가장 효율적인 계산 방법인 소수 세로셈 덧셈과 뺄셈 익히기입니다.
연산 연습은 이 방법을 익히는 것에 집중해야 합니다.
위 과정 공부를 끝낸 다음에는 실전 연습을 해야 합니다.
소수 덧셈과 뺄셈 문제해결력 기르기인데요.
아래 두 문제는 전국 기준 난이도 하 문제입니다. 무조건 풀 수 있어야 합니다.
초등학교 4학년이기 때문에 '읽기 능력'을 탓할 수도 없습니다. 아래 문제는 쉽게 풀 수 있어야 합니다.

만약 위 두 문제 중 한 문제라도 제대로 풀지 못했다면.. 총체적 난국 상황입니다.
상위권 대학은 생각할 수도 없고요. 웬만한 대학 진학도 어려울 것입니다.
물론 대학이 인생의 전부는 절대 아닙니다.
하지만 초중고 시기에 공부를 제대로 해 보는 경험은 정말 중요한데요.
그조차 점점 더 어려움을 느끼다가 수포자의 길로 들어서게 될 가능성이 높습니다.
만약 위 두 문제를 쉽게 풀었다고 하더라도 중상위권이라고 단정지을 수는 없습니다.
전국 기준 난이도 하 문제이기 때문에 이후 난이도 중하, 중중, 중상, 상상의 문제들을 충분히 풀어봐야 하는데요.
현재 아이의 전국 기준 실력이 어느 정도인지에 따라 어느 난이도의 문제를 주로 풀 것인지가 달라집니다.
그리고 전국 기준 상위권 대학을 노린다면 최소한 난이도 중상 문제들은 대체로 풀 수 있어야 하고요.
SKY나 서성한을 노린다면 상상(심화) 문제도 풀 수 있어야 합니다.

'연령(학년)별 공부 자료 > 초등 3~4학년' 카테고리의 다른 글
| [초등수학 4-2] '4. 사각형' 단원 제대로 공부하는 방법 (1) | 2024.10.10 |
|---|---|
| [초등수학 3-2] '4. 분수' 단원 교과서 공부 제대로 하는 방법 (1) | 2024.10.10 |
| [초등수학 3-2] '3. 원' 단원 교과서 핵심 개념 (3) | 2024.10.07 |
| [초등과학 공부법 4-2] 2. 물의 상태 변화 - 물이 더 클까? 얼음이 더 클까? (6) | 2024.10.05 |
| [초등수학] 시간과 시각, 오전과 오후, 진분수와 가분수 개념 제대로! (1) | 2024.09.24 |




댓글