[초등수학 6-2] '6. 원기둥, 원뿔, 구' 단원 제대로 공부하기
초등학교 6학년 2학기 수학 6단원은 '6. 원기둥, 원뿔, 구' 인데요.
<초등학교 6-2 수학 대단원>
1. 분수의 나눗셈
2. 소수의 나눗셈
3. 공간과 입체
4. 비례식과 비례배분
5. 원의 넓이
6. 원기둥, 원뿔, 구
'6. 원기둥, 원뿔, 구' 단원 교과서 내용의 핵심은 무엇일까요?
이 단원 공부는 어느 정도까지 해야 할까요?
이 단원은 매우 중요한 단원인데, 크게 어렵지는 않습니다.
완벽하게 이해하고 기억할 때까지 몇 번만 반복해서 공부하면 됩니다.
중등 수학과 연계도 되는 단원입니다.
우선 교과서에 나오는 개념과 원리부터 완벽하게 공부해야 하고요.
내신 문제집 풀면서 문제 해결력도 탄탄하게 훈련해야 합니다.
이를 위해, 이 단원의 교과서 핵심 내용을 정리했습니다.

우선 '원기둥' 이 나옵니다.
근데 원기둥이 무엇인지 아는 것은 어렵지 않습니다.
직관적으로 알 수 있도록 그림을 보여주기 때문이고요.
사전식 설명 개념은 나오지 않기 때문입니다.

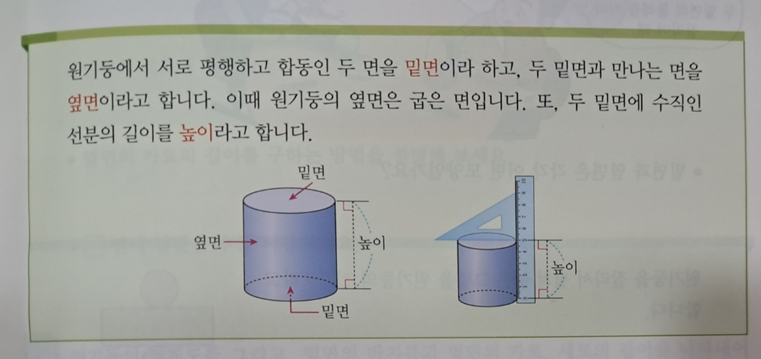
그 다음 원기둥에서 '밑면' 와 '옆면' 과 '높이' 개념이 나오는데요.
이 3가지 개념은 사전식 설명이 나오는데요.
◆ 밑면 : 원기둥에서 서로 평행하고 합동인 두 면
◆ 옆면 : 두 밑면과 만나는 면
◆ 높이 : 두 밑면에 수직인 선분의 길이
위 사전식 설명을 글자 그대로 완벽하게 암기할 필요는 없습니다.
하지만, 설명 내용을 읽고 완벽하게 이해는 할 수 있어야 하고요.
설명 내용과 비슷하게 말로 설명할 수는 있어야 합니다.
"원기둥에서 밑면이 뭐야?" 라는 질문을 받으면
"원기둥에서 평행하고 합동인 두 면" 이라고 이야기 할 수 있어야 합니다.
이 설명해서 핵심 키워드는 '평행' 과 '합동' 입니다.
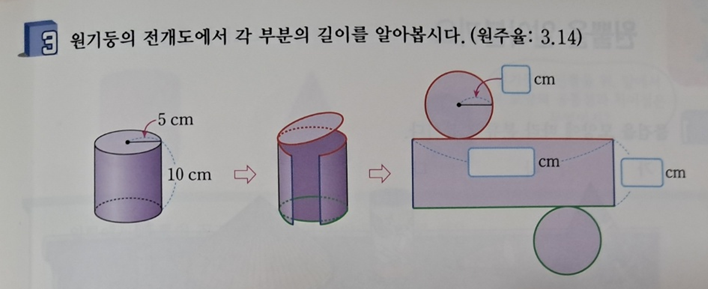
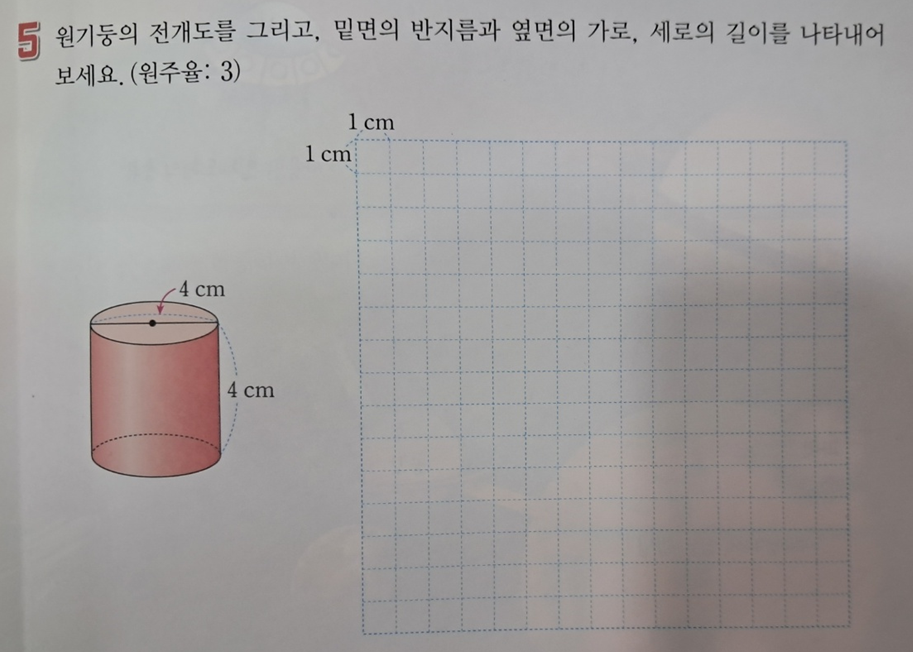
그 다음 '전개도' 가 나옵니다.
◆ 전개도 : 원기둥을 잘라서 펼쳐 놓은 그림
아래 개념 설명과 그림을 함께 보면 쉽게 알 수 있는 내용입니다.

그리고 아래 활동을 통해 전개도에 대한 이해도를 높이는 내용이 나옵니다.
아이가 직접 보고 생각하고 적용해 봐야 합니다.
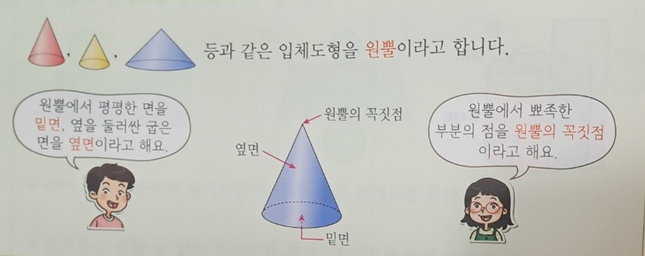
그 다음 '원뿔' 이 나오는데요.
원기둥처럼 직관적으로 알 수 있도록 그림을 함께 보여주기 때문에 쉽게 알 수 있는 내용이고요.
원뿔에서 '원뿔의 꼭짓점, 밑면, 옆면' 이 무엇인지도 함께 나옵니다.
모두 쉬운 내용이기 때문에 아이가 직접 읽고 확인하고 기억하는 것이 좋습니다.
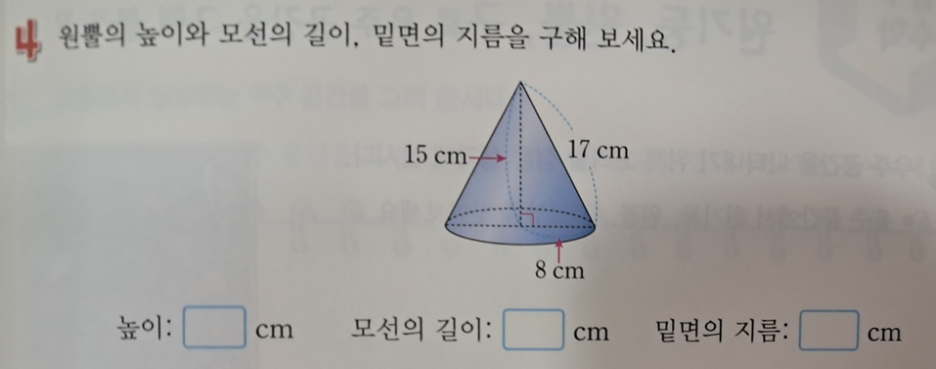
그 다음 원뿔에서 '모선' 과 '높이' 가 나오는데, 모선의 개념은 생각을 충분히 하면서 이해해야 합니다.
◆ 모선 : 원뿔에서 원뿔의 꼭짓점과 밑면인 원의 둘레의 한 점을 이은 선분
◆ 높이 : 원뿔의 꼭짓점에서 밑면에 수직인 선분의 길이
같은 '높이' 라고 하더라도 원기둥에서의 높이와 원뿔에서의 높이 개념이 다릅니다.
이 차이를 잘 파악해야 합니다.
◆ 원기둥에서의 높이 : 두 밑면에 수직인 선분의 길이
◆ 원뿔에서의 높이 : 원뿔의 꼭짓점에서 밑면에 수직인 선분의 길이

그 다음 '구' 가 나오는데요.
원기둥과 원뿔 때처럼 직관적으로 알 수 있게 하는 수준이라 쉽습니다.

그리고 '구의 중심' 과 '구의 반지름' 이 나옵니다.
두 개념 모두 완벽하게 이해해야 합니다.
◆ 구의 중심 : 구에서 가장 안쪽에 있는 점
◆ 구의 반지름 : 구의 중심에서 구의 겉면의 한 점을 이은 선분

여기까지 하면 교과서 개념 학습이 끝나고요.
이제 문제를 풀면서 내신 문제해결력을 길러야 하는데요.
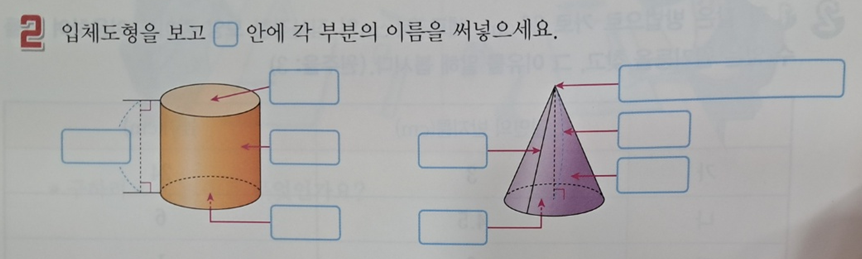
아래 문제는 교과서 문제들입니다.
모두 쉬운 기초 문제이기 때문에 쉽게 풀 수 있어야 하며,
아래 문제까지 잘 풀면 교과서 공부가 끝난 것입니다.
만약 아래 문제를 풀지 못하거나 헷갈리는 부분이 있다면,
교과서 공부를 다시 복습해야 합니다.

여기까지가 수학 교과서 공부를 제대로 한 것이 되고요.
그 다음에는 학기 당 내신 문제집 2권을 풀면서 내신 문제해결력을 더 훈련해야 합니다.
이때 상위권이 목표라면 최소한 준심화 수준의 문제집은 만만하게 풀 수 있어야 합니다.
'연령(학년)별 공부 자료 > 초등 5~6학년' 카테고리의 다른 글
| [초등수학 6-2] '1. 분수의 나눗셈' 단원 대표 유형 문제 풀어보기 (0) | 2024.11.20 |
|---|---|
| [초등수학 5-2] '1. 수의 범위와 어림하기' 단원 대표문제 풀어보기 (0) | 2024.11.18 |
| [초등수학 5-2] '6. 평균과 가능성' 단원 공부 제대로 하기 (0) | 2024.11.11 |
| [초등수학 5-2] '6. 평균과 가능성' 교과서 공부부터 제대로 하기 (3) | 2024.11.10 |
| [초등수학 6-2] '5. 원의 넓이' - 엄청 중요한 단원 (0) | 2024.11.05 |




댓글