[초등수학 3-2] '1. 곱셈' 단원 대표 유형 문제 풀어보기
초등학생 때 아이의 수학 실력을 결정하는 것은 무엇일까요?
개념과 원리를 잘 알고 있는 것일까요? 아닙니다.
연산(계산)을 잘 하는 것일까요? 아닙니다.
둘 다 중요한 항목이지만 아이의 수학 실력을 결정하는 것은 아닙니다.
개념과 원리만 잘 알고 있다고 해서 좋은 성적을 얻게 되는 것도 아니고요.
연산(계산)을 잘 한다고 해서 좋은 성적을 얻게 되는 것도 아닙니다.
최종적으로 아이의 수학 실력을 결정하는 것은 '문제 해결 능력' 입니다.
그래서 다양한 유형과 적절한 난이도의 문제들을 충분히 풀어보는 것이 매우 중요한데요.

이는 초등뿐만 아니라 중등과 고등 때에도 마찬가지이고요.
학교 내신 시험이나 수능 시험 때에도 마찬가지입니다.
그리고 다양한 유형의 문제를 풀어볼 때에는 먼저
각 단원별 대표 유형 문제들부터 잘 풀어봐야 합니다.
아래 문제들은 초등학교 3학년 2학기 수학 1단원인 '1. 곱셈' 단원에서 대표 유형에 해당하는 문제들입니다. 물론 아래 4문제 말고도 대표 유형 문제는 더 있는데요.
일단 이 문제들을 통해 현재 아이의 문제 해결 능력을 체크해 보시기 바랍니다.
대표 유형 문제 1

위 문제는 '1. 곱셈' 단원에서 가장 기본 유형에 해당하는 문제입니다.
난이도는 전국 기준으로 중간보다 아래 문제이고요. 이 정도 문제는 반드시 풀 수 있어야 합니다.
대신, 아이가 이 문제를 쉽게 잘 풀었다면,
이 난이도의 이 유형 문제는 더 풀어볼 필요가 없습니다.
(풀이)
동화책의 수 35×43 = 1505권
위인전의 수 28×17 = 476권
참고서의 수 2500-1505-476 = 519권
대표 유형 문제 2

위 문제도 자주 나오는 유형의 문제인데요.
초등학교 1~2학년 때 수 카드를 주고 가장 큰 수 만들기 문제처럼 생각하면 틀립니다.
위 문제에서 곱이 가장 크게 하려면 두 자리 수의 십의 자리에 8, 7을 놓아야 합니다. (이 생각을 해야 합니다!)
(풀이)
83×72 = 5976
82×73 = 5986
곱이 가장 큰 곱셈식은 82×73 = 5986
대표 유형 문제 3

위 문제도 이 단원의 대표 유형 문제입니다.
그리고 이런 유형의 문제는 수학적 사고력이 괜찮아야 풀 수 있는 문제입니다.
그래서 이 문제를 잘 풀면, 수학을 잘 할 가능성이 크고요.
만약, 곱셈 계산은 잘 하는데, 이 문제를 잘 풀지 못하고, 설명을 들어도 잘 이해하지 못하면..
현재 수학적 사고력과 문제 해결력이 약한 상태일 것입니다.
(풀이)
어떤 수 : □
잘못 계산한 식 : □-26 = 48
□ = 48+26 = 74
바르게 계산하면 74×26 = 1924
대표 유형 문제 4
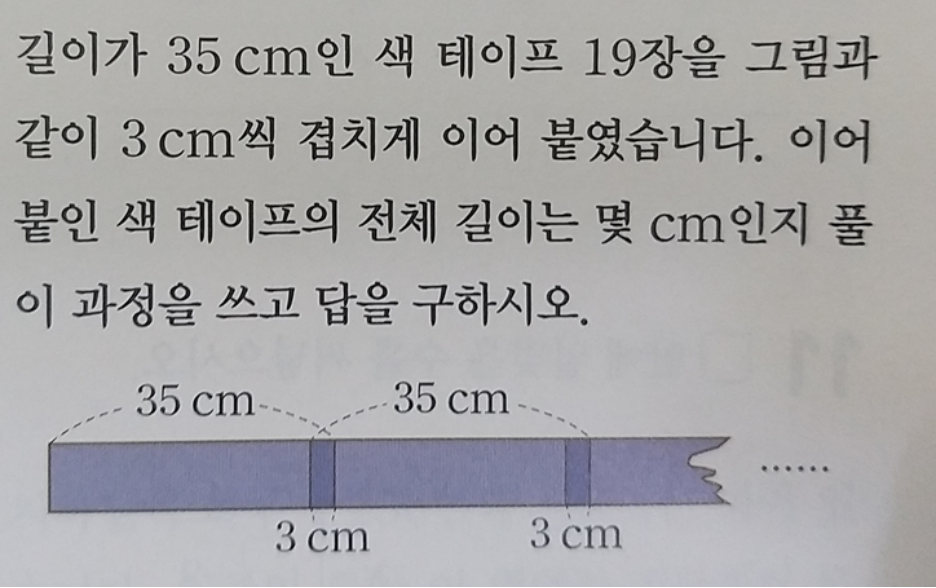
위 문제는 수학적 사고력도 좋고, 내신 문제 해결력도 좋아야 풀 수 있는 문제입니다.
이 유형의 문제를 처음 만났는데 쉽게 풀었다면, 전국 기준 상위권에 들 가능성이 충분한 상태로 생각됩니다.
(풀이)
색 테이프 19장의 길이의 합 : 35×19 = 665m
겹쳐진 부분의 길이의 합 = 3×18 = 54m
이어 붙인 색 테이프의 전체 길이 : 665-54 = 611m
앞으로 초중고와 대입 모두 과목별 내신 서술형 논술형이 강화됩니다.
그래서 단순 계산, 단순 암기 위주의 공부는 별 도움이 되지 않고요.
제대로 읽고, 제대로 이해하고, 제대로 기억하고, 제대로 풀어보고 설명해 본 아이들이 잘 하게 될 것입니다.

'연령(학년)별 공부 자료 > 초등 3~4학년' 카테고리의 다른 글
| [초등수학 4-2] '2. 삼각형' 단원 대표 유형 문제 풀어보기 (0) | 2024.11.29 |
|---|---|
| [초등수학 4-2] '1. 분수의 덧셈과 뺄셈' 단원 대표 문제 (0) | 2024.11.17 |
| [초등과학 공부법 3-2] 4. 소리의 성질 - 높은 소리, 낮은 소리, 반사되는 소리 (0) | 2024.11.13 |
| [초등수학 4-2] '6. 다각형' 교과서 공부 제대로 하기 (0) | 2024.11.09 |
| [초등수학 3-2] '6. 자료의 정리' 단원 효율적인 공부 방법 (1) | 2024.11.08 |




댓글