[초등수학 4-2] '5. 꺾은선그래프' 교과서 공부부터 제대로 하기
초등학교 4학년 2학기 수학 5단원은 '5. 꺾은선그래프' 단원입니다.
이 단원의 교과서 내용은 쉽습니다.
그래서 교과서 공부 어렵지 않게 제대로 공부하고,
내신 문제집 문제 잘 풀어보면 됩니다.
난이도가 매우 높은 문제를 만드는 것이 쉽지는 않은 단원이어서,
내신 문제집 선택만 잘 하면, 무난하게 공부할 수 있는 단원입니다.
<초등 4학년 2학기 수학 6개 대단원>
1. 분수의 덧셈과 뺄셈
2. 삼각형
3. 소수의 덧셈과 뺄셈
4. 사각형
5. 꺾은선그래프
6. 다각형
이 단원의 교과서 핵심 내용은 다음과 같습니다.

우선 '꺾은선그래프' 가 무엇인지 개념 정리가 나옵니다.
역시나 완벽한 개념 공부란 해당 개념을 설명할 수 있을 정도까지 공부하는 것인데요.
아래 개념을 암기하고 이야기하는 것은 단순무식 방식이고요.
개념을 이해한 다음에, 설명 내용이 아래 교과서 내용과 조금 다르더라도 직접 생각해서 이야기하는 방식이 좋습니다.
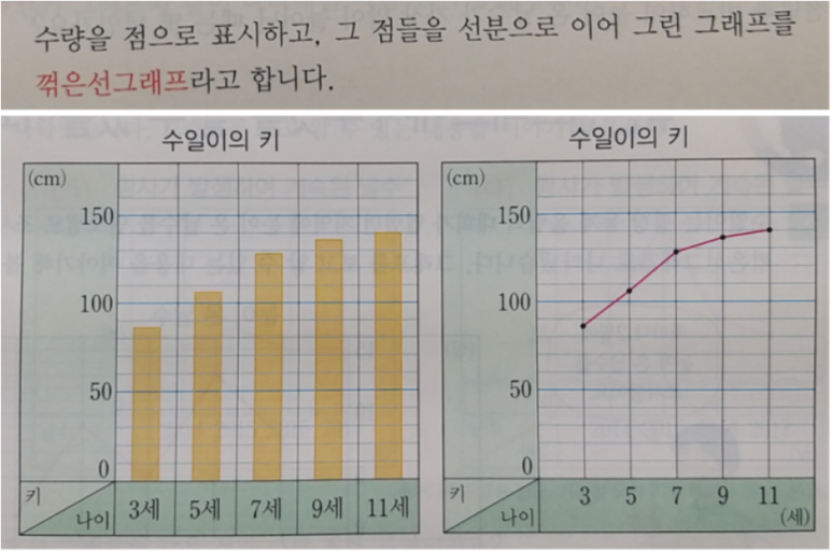
아래 두 그래프에서 오른쪽 그래프가 꺾은선그래프입니다.
◆ 꺾은선그래프 : 수량을 점으로 표시하고, 그 점들을 선분으로 이어 그린 그래프
아래 그래프에서 왼쪽이 막대그래프이고, 오른쪽이 꺾은선그래프입니다.
난이도 차이가 크진 않고요.
그래프의 종류를 알고, 그래프를 읽을 수 있으면 됩니다.
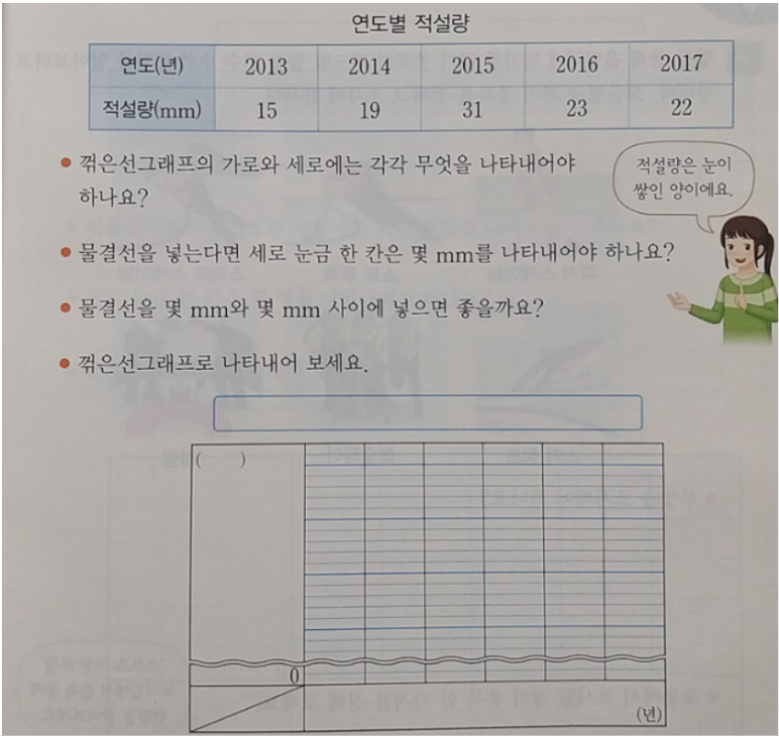
그 다음 핵심 내용은 꺾은선그래프를 그리는 방법을 공부하는 것입니다.
사실 아래 교과서 내용도 그리 어렵지 않습니다.
지금까지 수학 공부를 제대로 하기만 했다면 아이 스스로 충분히 이해할 수도 있고,
그래프를 그릴 수도 있습니다.
지금까지 교과 공부를 통해 기른 수학적 사고력만으로도 충분히 공부할 수 있는 내용입니다.
그리고 그래프 아래쪽에 물결처럼 보이는 부분은,
그래프의 세로 길이가 너무 길어서 일부 생략한 부분이라는 것만 이해하면 됩니다.
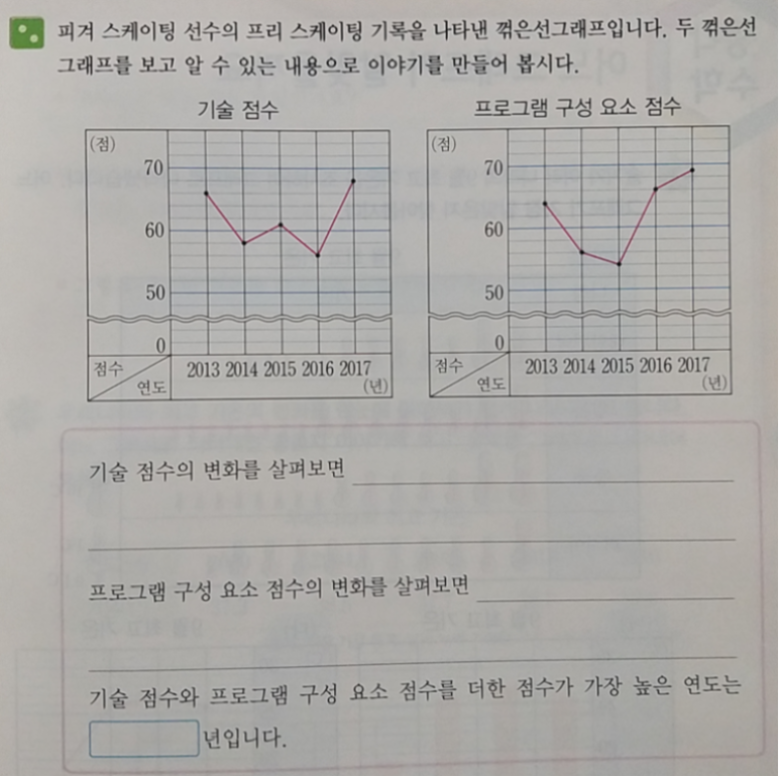
그 다음 핵심 내용은 주어진 꺾은선그래프를 읽고 분석하는 연습을 하는 내용인데요.
난이도가 높지는 않지만.. 계산 위주로만 공부한 아이라면, 설명이나 표현에 익숙하지 않아서 막막하게 느껴질 수 있습니다. 이 경우에는 구체적인 사례를 두 세번 정도 읽으면 도움이 될 것입니다.
아래 꺾은선그래프 중 기술 점수 그래프를 보면, 2013년부터 2016년까지는 대체로 점수가 내려갔지만 2017년에 다시 크게 올라간 것을 알 수 있고요.
프로그램 구성 요소 점수 그래프를 보면, 2013년부터 2015년까지는 점수가 내려갔지만 2016년과 2017년에는 다시 올라갔을뿐만 아니라 크게 향상된 것을 알 수 있습니다.
위 내용이 교과서 핵심 내용의 전부입니다.
꺾은선그래프가 무엇인지 알고, 꺾은선그래프를 그릴 수 있고, 꺾은선그래프을 읽고 분석할 수 있으면 이 단원 교과 공부는 다 한 것이고요.
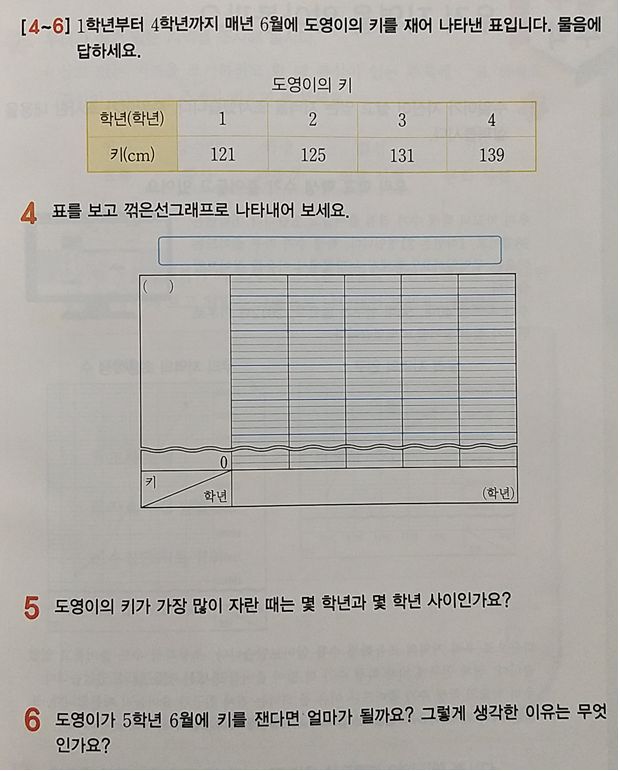
이제 문제해결력 훈련을 해야 합니다. 아래 문제는 교과서 문제이고요.
난이도는 전국 기준 하 수준입니다. 즉, 아래 문제는 반드시 풀 수 있어야 합니다.
'초등수학 공부법' 강.의 때 "자료와 가능성 영역은 초등학교 4학년까지도 그리 어렵지 않습니다. 수와 연산 영역, 도형 영역 공부만 제대로 하면 그 힘으로 자료와 가능성 영역도 잘 하게 됩니다." 라고 말씀 드립니다.
그러니 만약 저학년이라면 수와 연산 영역 제대로 공부에 집중하시고요.
중학년이라면 수와 연산 영역과 도형 영역 제대로 공부에 집중하시기 바랍니다.
그러면서 측정 영역만 잘 챙기면 나머지 영역 공부는 자연스럽게 잘 하게 될 것입니다.
그리고 아이의 내신 문제 해결력을 기르기 위해서는
한 학기 당 내신 문제집 2권 정도 푸는 것을 추천합니다.
이때 현재 아이의 전국 기준 실력이 어느 정도인지에 따라
어느 난이도의 문제집을 풀 것인지가 달라집니다.
그리고 전국 기준 상위권 대학을 노린다면
난이도 준심화~심화 문제들은 대체로 풀 수 있어야 하고요.
SKY나 의대, 치대를 노린다면 상상(심화) 문제 이상도 풀 수 있어야 합니다.
'연령(학년)별 공부 자료 > 초등 3~4학년' 카테고리의 다른 글
| [초등과학 공부법 3-2] 4. 소리의 성질 - 소리란 뭘까? 큰 소리란? 작은 소리란? (0) | 2024.10.27 |
|---|---|
| [초등과학 공부법 4-2] 3. 그림자와 거울 - 빛과 그림자 (초등과학 홈스쿨링) (3) | 2024.10.26 |
| [초등수학 공부법 3-2] '5. 들이와 무게' - 들이, 무게 단위 공부 잘 하기 (1) | 2024.10.22 |
| [초등과학 공부법 3-2] 공기란 무엇인지 쉽게 이해하기 (1) | 2024.10.21 |
| [초등수학 3-2] '4. 분수' 단원 교과서 공부 제대로 하기 (2) | 2024.10.20 |




댓글