[초등수학 5-2] '3. 합동과 대칭' 교과서 핵심 내용
초등학교 5학년 2학기 수학 3단원은,
'3. 합동과 대칭' 단원입니다.
이 단원은 초등 수학에서 중요한 단원이고요.
중등 수학 공부에도 영향을 주는 단원입니다.
다행히 교과서에 나오는 개념이 어렵지는 않습니다.
하지만 쉬운 개념도 아닙니다.
그래서 개념 공부를 할 때 제대로 해야 하고요.
단원 공부가 끝나도 한 두번 더 개념 복습을 하는 것이 좋습니다.
먼저 교과서나 문제집에 있는 개념 정리를 읽고 이해해야 하고요.
그 다음, 각각의 사례에 적용하면서 설명까지 할 수 있어야 합니다.
이를 위해 이 단원의 핵심 개념이 무엇인지 정리했습니다.

<초등학교 5학년 2학기 수학교과서 목차>
1. 수의 범위와 어림하기
2. 분수의 곱셈
3. 합동과 대칭
4. 소수의 곱셈
5. 직육면체
6. 평균과 가능성
이 단원에 나오는 수학 용어들의 개념을 완벽하게 이해하고 기억해야 하는데요.
가장 먼저 나오는 개념은 '합동' 입니다.
* 합동 : 합할 합(合) + 한 가지 동(同)
'합동' 은 한 가지(하나)가 되는 경우입니다.
한 가지가 되려면, 하나가 되려면 모양도 같아야 하고, 크기도 같아야 합니다.
* 합동 : 모양도 같고, 크기도 같아서 완전히 겹치는 두 도형

그 다음에는 대응점, 대응변, 대응각이 나오는데요.
'겹치는' 이 핵심입니다. 자칫 헷갈릴 수 있습니다.
초등 5학년 아이들에게 '대응' 이라는 어휘는 쉽지 않은 어휘입니다.
두 도형을 포개었을 때 완전히 겹친다는 것이 어떤 것인지를 한 번만 직접 해 보면 쉽게 이해할 수 있고요.
아래 개념 정리를 천천히 읽으면서 정확하게 이해하는 것이 중요합니다.
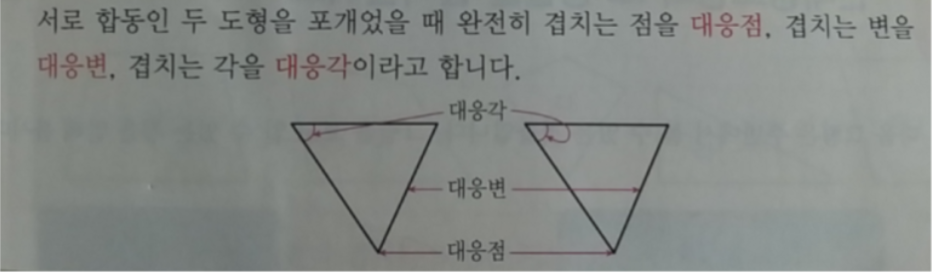
* 서로 합동인 두 도형을 포개었을 때 완전히 겹치는 점을 대응점, 겹치는 변을 대응변, 겹치는 각을 대응각이라고 합니다.
그 다음에는 선대칭도형과 대칭축이 나오는데요.
이 내용도 한 번만 직접 해 보면서 이해하면 훨씬 쉽게 이해할 수 있습니다.
직접 해 보는 데 시간이 많이 걸리지도 않습니다.
학교에서든 학원에서든 집에서는 개념 공부를 할 때 직접 해 보면서 정확히 이해하는 것이 핵심입니다.
* 한 직선을 따라 접었을 때 완저히 겹치는 도형을 선대칭도형이라고 합니다. 이때 그 직선을 대칭축이라고 합니다.

그 다음 점대칭도형과 대칭의 중심이 나오는데요.
위 개념들과 비교하면 조금 어려운 개념입니다.
역시나 가장 효과적인 방법은 직접 해 보는 것입니다.
직접 해 보면서 왜 90도 돌리면 겹치지 않고 180도 돌리면 완전히 겹치는지 확인하면서 이해하는 게 좋습니다.
* 한 도형을 어떤 점을 중심으로 180도 돌렸을 때 처음 도형과 완전히 겹치면 이 도형을 점대칭도형이라고 합니다. 이때 그 점을 대칭의 중심이라고 합니다.

만약 이 단원에 나오는 '합동, 대응점, 대응변, 대응각, 선대칭도형, 대칭축, 점대칭도형, 대칭의 중심'의 개념을 확실하게 알지 못하면.. 이후에 나오는 교과서 문제와 익힘책 문제를 제대로 풀 수 없습니다. 즉, 공부 자체를 할 수 없는 거죠.
그래서 우선 교과서 수학 용어의 개념부터 정확하게 이해하고 암기해야 하고요.
그 다음 교과서와 익힘책에 나오는 문제를 제대로 풀어봐야 합니다. 여기까지가 기초, 기본 공부에 해당합니다.
그 다음 해야 할 것은, 이 단원에 해당하는 난이도 중중, 중상, 상상(심화) 문제들을 차근차근 풀어봐야 하는데요.
아래 문제는 전국 기준 난이도 중하~중중에 해당하는 문제입니다.
초1 수학이 아니라 초5 수학이기 때문에 문과, 이과 관계 없이 아래 난이도 문제는 쉽게 풀 수 있어야 합니다.

초등 5학년 2학기 시기는, 수학 선행을 시작하거나 이미 시작한 상태여야 합니다.
그리고 SKY나 서성한, 이공계열 중경외시를 목표로 한다면 심화까지 선행해야 하고요.
인문학계열 중경외시나 건동홍숙 수준을 생각한다면 준심화까지는 선행을 해야 합니다.
그리고 선행에 심화 또는 준심화까지 할 수 있으려면 먼저 자기 학년 수학을 심화 또는 준심화까지 할 수 있어야 합니다.
즉, 5학년 2학기 시기에는 심화 또는 적어도 준심화까지 풀어야 들어 본 대학 이상을 목표로 할 수 있습니다.
우리나라에서 수학 잘 하는 방법은 복잡하지 않습니다.
교과서 공부 제대로 하고요. 학기 당 내신 문제집 2권 풀면서 초등 4~5학년 때 내신 문제 준심화 이상을 풀어내면 됩니다.
근데 그 수준까지 안 되는 초등 5학년이 절반이 넘습니다..
교육부에서 2028년 대입개편안을 발표한 후로,
중등뿐만 아니라 초등과 유치까지 혼란과 마케팅이 급속도로 퍼지고 있습니다.
블로그뿐만 아니라 유튜브와 인스타를 통해
정확한 정보와 마케팅이 뒤섞여 있는데요.
이럴수록 비판적인 정보 수용이 중요하고요.
앞으로 유아~초등 공부에 어떤 변화가 생길지,
어떤 기준으로 해석하고 분석해야 하는지,
가장 현명하고 효율적인 대비 방법은 무엇인지 정리해 드리고 있습니다.
행공신 블로그와 온오프라인 강.의와 컨설팅을 총 동원하고 있습니다.
꼭 참고해 보세요. 많은 궁금증이 해결되실 거예요~ ^ㅡ^
[10월 강.의안내] 급변하는 대입과 초등 대비법 (2028년 대입개편안)
https://blog.naver.com/jnanna89/223580022753
[학습코칭] 진한 감동을 주신 학원 원장님의 컨설팅 후기 문자 T.T
https://blog.naver.com/jnanna89/223490742021
온라인 오프라인 '전국 컨설팅' 을 진행합니다!
https://blog.naver.com/jnanna89/223411183581
온라인 오프라인 '전국 컨설팅' 을 진행합니다!
안녕하세요! 정용호 강사입니다! 1:1 맞춤으로 아이 공부 플랜을 정리해 드리는 컨설팅을 진행합니다. ∎ (...
blog.naver.com


'연령(학년)별 공부 자료 > 초등 5~6학년' 카테고리의 다른 글
| [초등수학 5-2] '4. 소수의 곱셈' 원리부터 완벽하게 공부하기! (3) | 2024.10.13 |
|---|---|
| [초등수학 6-2] '2. 소수의 나눗셈' 교과서 핵심 원리 제대로 공부했나? (1) | 2024.10.08 |
| [초등한국사 공부법 51] 신라 '동궁과 월지' 이름 해석하기! (0) | 2024.08.23 |
| [초등한국사 공부법 50] 신라 바다의 왕은 장보고! 발해 교류 (한국사능력검정시험 대비) (0) | 2024.08.16 |
| [초등한국사 공부법 49] 중동과도 교류한 신라, 원효대사 이야기 (한국사능력검정시험 대비) (0) | 2024.08.09 |




댓글